Things I have had to do to do experiments

I was talking to my friend Michelle the other day about all the various things I have experienced on the way to gathering data for research. Lately, I've been watching a lot of Discovery Channel shows about various odd and dirty jobs people have, and also those shows about those crazy academics who go out in dangerous waters infested with killer jellyfish. It makes me realize, wow, I'm glad I wasn't stupid enough to choose a topic that almost kills me. But I have had my moments. Here are a few:

The peeing baby incident: That time when I was conducting research on infants' vision, a mother had to change her baby's diaper. In the midst of doing this, I turned to give the mother privacy and was working on my computer. Suddenly, I felt this weird wet sensation down my back and turned. Yup, you can fill in the rest of this story, but I was on the receiving end of a 6 month old's golden shower. I wonder if this baby (who must be about ten years old now) knows that he pissed all over some poor grad student at Chicago.

The vomiting RA: One time in Chicago, I had an experiment where I needed a confederate, someone who is pretending to be a naive subject but is actually in on the game. My RA came in the lab on a Saturday morning reeking of bar (stale cigarette smoke, cheap beer). She was still drunk. She apologized, and just as the subject showed up, vomited into her hands, which seemed to make things worse, spraying the flow and all over me and my laboratory. Just as the subject was coming in. Needless to say, she didn't last long after that.

The forgotten subject: This one didn't happen to me, but I caused this one to happen. One time, I had a friend of mine come in for an experiment in which the participant decided whether a particular fish was a member of category A or B on a self-running computer program. You see examples of fish on the screen and have to classify them as A fish or B fish, until you get 25 correct classifications in a row, at which point the experiment ends. I started this friend of mine, then somehow got distracted and forgot about him. Most people got the 25 correct in a row in about twenty minutes. Five hours later, I walk into the room for another reason, only to find my friend still at the computer, head in his hands, classifying fish. He got up and started screaming that he was going to Fing knock my Fing teeth out of my Fing mouth if I Fing make him Fing classify Fing anotherFing one of these Fing Fing fishes. I actually had to edit that - he said it with a lot more F bombs. He never let me forget that fish experiment. I think he is still scarred.

Chimp piss: When I was in Japan, I visited the National Primate Research Institute, where they have chimps. While watching one experiment, a baby chimp climbed to the top of his cage. I was about two feet away from him. He then let forth a violent spray of urine, covering me. Interestingly, that was the day I actually peed my own pants the next day, a story you can read about here.

Baby vomit. I was holding a baby for my experiment and it burped, then a little swish sound, and that familiar warmth down my back. I gotta stop working with babies!

There are probably other stories I have locked in the vaults of memory. I'll post any if I remember. Always remember - Don't due this at home. We're what you call, "professionals."

Overheard

I was talking with Matt, a friend of mine, last night. We were speaking about those people who are simply oblivious to the fact that they are completely obnoxious. In the course of the conversation, he said...

"You have a real problem when the biggest problem you will have to face in your entire life is you."

I have to say, never have truer words been spoken.

Finding the missing piece

Summer is time for love, and I offer you an analysis of the probability of meeting your soul mate. In his Symposium, Plato writes that people were originally both male and female. To prevent them from acquiring the power of the Gods, Zeus cut them in half. Life then became for humans a search for the other half that was lost, in order for them to once again attempt to ascend Mount Olympus.

It is a pretty story, and one that resonates with many a New Age follower’s conception of love. Even if it doesn’t quite jive with reality. But why not?

The reason once again has to do with probability. There is a well known problem in the statistics literature called the Birthday Paradox. Basically, the paradox questions, “How many people do you need to put into a room to get a 50% chance that two of the people have the same birthday?” The answer to this is 23. Therein lies the paradox – this seems like a very small number. Most people intuitively think that one needs to have 365/2 or 183 people in the room. But that intuition is wrong. The true formula is as follows:

N = .5 + SQRT((.25 + 2 * 365 * ln(2))

I would like to generalize this problem to the question of finding one’s soul mate. Specifically, the question I address is how many people would you have to include in a room for there to be a 50% chance that any two people in the room were once joined at the hip before Zeus took his shears and sliced them apart? Now, this assumes that the people in the room were randomly selected from the entire world population, which is approximately six billion people. The answer to this is simple, and follows the formula above:

N = .5 + SQRT((.25 + 2 * 6,000,000,000 * ln(2)) = 91,202

Wow! It would take a room of 91,202 people for there to be a 50% chance that any two people in that room were actually soul mates. One would have to have a pretty big room, perhaps as large as this room, which fits over 100,000 people.

Imagine a speed dating service in which you have five minutes to talk with every other person in this room. For those two lucky halves to actually have a chance to meet, the speed dating round would have to last for 91,202*5 minutes, which comes out to 316.67 days. All for only two of those 91,202 people to meet. This says nothing of the 91,200 people who leave Michigan Stadium brokenhearted or satisficing with someone who is not their other half.

But that doesn’t help you, dear reader, who doesn’t care about any two people encountering their soul mate, but rather about the probability that YOU will meet your soul mate. Well, the problem is that to calculate this, one would require a supercomputer that can handle a hell of a lot more decimal places than my humble Dell laptop. Needless to say, you would need a room about as big as this place to have a 50% chance of meeting your other half.

What does this tell you? Well, quite simply, you have about as much of a chance of meeting your other half as you do winning the powerball lottery. Either that, or the search for love isn’t a search for that one soul mate that Zeus cut from your side, but that any of a number of possible other halves fit approximately well enough that they can serve as soul mates. I tend to believe this is the case, because I know many a person who has claimed to have met their soul mate, and I know the probability of this actually occurring has about a snowball’s chance in hell. And whether or not I believe in soul mates matters very little. I do believe in probability!

But I tend to be hopeful. And I am a romantic who enjoys Greek mythology. I know my other half is wandering around out there. Of this I am certain beyond any statistical doubt. Whoever she is, I know she would appreciate my calculation of the infinitesimally small likelihood that we would ever meet.

Experimentaholic discovers a new force in the universe!

Leg day. There is nothing worse than leg day.

So ever since my semester ended, I have been spending more time at my gym. I generally don’t have much time for working out during the semester, but summer means time to try and avoid the ravages of time by exercise. Once you turn 25 apparently you lose a pound of muscle and gain a pound of fat per year. Lord knows I’m fat enough already to know that I don’t need another pound of fat come January, so there I go. But the other day I was really annoyed about going, since it was leg day.

Leg day is the day everyone hates, the day when you throw several hundred pounds on the barbell and do squats, or hold dumb bells and do lunges. Arm day is easy. Leg day just blows. But one thing I have noticed recently is that most men skip the leg exercises. They have skinny legs but massive chests and arms, which is obviously because they only do chest and arm exercises. But women don’t seem to skip those leg exercises – there are generally many women doing the ass and thigh machines. With one exception.

Over a month ago, when I started to go to the gym more regularly, I ran into this woman named Kelly. Kelly is stunningly beautiful. Tall, dark hair, gorgeous eyes, she could be mistaken for an actress. (She is actually a fashion model and aspiring actress…I know this only because we once got into a conversation because we were both wearing the same university tee shirt.) Kelly is one of those women who does her leg exercises quite regularly. And suddenly one day I noticed something rather perplexing about the nature of the universe. First, I noticed Kelly was doing her leg exercises. But then I noticed that there were several men, also doing leg exercises. I thought, “Wait a minute – that section is usually empty!” The next day…same thing. The following day, yet again.

Then, I had an epiphany. Maybe there is a new physical force in the universe, akin to gravity, that emanates solely from Kelly. Let’s call it the Kelly Field. It is a physical force that somehow attracts men to go to the leg section of the gym and work away those chicken-legs. I felt like Newton, but instead of an apple that struck me, it was a dumb bell.

I began to wonder how I could test whether Kelly was the source of a new force field that should be further investigated by more empirical studies, or whether this effect was merely due to chance or coincidence. So I designed a little experiment to test the hypothetical existence of the Kelly Field. Whenever I saw Kelly doing leg exercises, I counted the number of men and the number of women who would also be doing leg exercises. But after about two seconds of thinking, I realized this is not a very good experimental design: One needs a control condition. Maybe it is the case that when anyone – not just Kelly - goes into the leg section, that it attracts men to that section of the gym. So I had to have an alternative hypothesis…the existence of a Experimentaholic Field. If it were the case that anyone going to the leg section would attract men, then when I go to the leg section I would find just as many men working their legs as when Kelly was working out in that section. So I simply began to count the number of men in the leg section when Kelly was working out there, and the number of men when I was working out there. I eliminated a possible confound by never doing leg exercises when Kelly was doing leg exercises. Unlike other men, I was somehow unaffected by this force field, or at least could resist it at times.

At the end of three weeks, I had tallied the following totals over the course of 10 observations of Kelly and Experimentaholic. Below is a chart with the actual counts

Kelly: Men = 20, Women = 14

Experimentaholic: Men = 3, Women = 18

As can be seen in the contingency table above, there were far more men doing leg exercises in the presence of Kelly than in the presence of Sean. But this could be due to chance, right? How can one tell?

Well, the British statistician Karl Pearson saved the day when he came up with the formula for the Chi-Square test. Chi square allows you to determine whether there are associations among binary variables are likely to be due to chance. I ran the test, and found that the Chi Square test showed that the probability of such a large discrepancy in the number of men versus women working on their legs in the presence of Kelly versus Sean being due to chance is extremely low…like one in ten thousand. So the effect is real: there actually is a Kelly Field.

I wonder about the mechanism behind the Kelly Field. Does it work like gravity, and that its effect is a function of the squared distance between Kelly and men? Or is it something more like magnetism? Will we someday be able to throw out the theory of the Kelly Field and replace it with a Quantum Kelly Relativity Theory? Or a String Theory of Kelly? Only further investigations into the Kelly Field will provide us with these answers.

Currently I am working on my manuscript for the journal Science about this.

Actually, I’ll get to it once I get back from the gym.

What 3600 feels like

The number of American soldiers who have been killed in Iraq is rapidly approaching 3600. I knew none of them, but I know that none of them deserve to be included in a number as massive as 3600. But what do such massive numbers mean? I think we are used to the physical reality of small numbers. We can think about 5 or 10 or 100 in real terms, because these are sets of objects that are common in our daily life experiences.

Sure, you may be thinking, I paid $300,000 for my house...but I am sure you didn't pay it in ones you've been stuffing in your mattress from the tip jar at the coffee shop where you may work, counting it out one by one. Money was electronically transferred between financial institutions in less than a second. Every once in a while, we find a box of 500 nails, or 1000 plastic bags, but even then, we don’t often really have an experience with all 500 or 1000 at once. Over the years you use the nails one or two at a time, or accumulate the bags in your drawer, in batches of 5 or 10 every time you go to the store. You don't really have a sudden understanding of 1000 bags until the sleepless night you take them from your drawer and put them in a pile, or 500 nails until you accidentally knock them on the floor and have to pick each and every one up.

Perhaps an understanding through analogy, temporality, spatiality?

Sit still for one hour and count, one number a second. At the end of that long and boring hour, you will hit 3600.

See the sea of periods below? That is 3600 periods.

........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................
........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................ ........................................................................................................................

3600 is the number of days in 9.86 years.

Want to drive from New York to Los Angeles? Drive 3600 miles west and you'll end up in the Pacific Ocean, because L.A. is only 2800 miles from New York.

Want to build a time Machine and go back and have a long chat with Socrates (I would like to give him a piece of my mind about that whole thing about physical reality not mattering)…go back 3600 years and you’ll have overshot him by about 800 years. In fact, you would have also missed Ancient Greece and have ended up in one of Homer’s stories.

One of the folks who visits my site has a project on plastic bags with a counter of the number of plastic bags used so far this year. Last I checked it was up to 231,253,112,013. Which is far more than the number of seconds I have lived this far in my life (I am 30): 480,924,000.

How do we think about such large numbers? How can we make large numbers more accessible to our reasoning so that we can think better about quantities Because I want a subjective experience of a large number that carries representational heft. I want to know what 200,000 feels like when someone tells you that over 200,000 people died in the atomic bombings in Hiroshima and Nagasaki, or what 800,000 feels like when I am told that the Rwandan genocide killed up to 800,000 people, or what 6 million feels like when I am told that 6 million people died in the holocaust?

And I want to feel what 3600 feels like when I discover that 3600 Americans have sacrificed their lives in the Iraq war.

What's the meaning of your life?

Last year I was asked to give a speech at a dinner for my school's psychology honor society. I just stumbled across it today and figured I would put it out there.

Thank you for inviting me today. It truly is an honor to speak to you on this special day when you join the prestigious group of psychologists who comprise this honor society. I know I speak for the faculty in saying that we are proud of your accomplishments and enjoy having you all in our classes and laboratories.

As psychologists, we often ask ourselves questions. And at some point, as human beings, most of us have asked ourselves the biggest question out there: what is the meaning of life. If you attempt to find an answer to this question, I’m sure you will become frustrated fairly quickly, because you may find there are so many smaller questions that have yet to be answered. And without answers to the smaller questions, you can’t even begin to approach the most massive question of all.

So today I want to tell you about a question so seemingly insignificant that you probably have never thought about it before. However, trivial as it might seem, it has taken up a majority of the past 5 years of my life, and I still believe that I might understand perhaps less than 5 percent of the answer. So the question is this: how do we come to understand that objects have size. To answer this question one must first consider the history of how we have conceptualized the process of cognitive development.

A long standing belief in the history of philosophy and psychology is that infants come into the world with few cognitive abilities or skills. This is best captured by the British Empiricist philosopher John Locke’s proposal that the infant mind is a tabula raza, a blank slate. Locke claimed that experience writes all knowledge upon this slate. This perspective led William James to claim that the infant experiences the world as a blooming, buzzing confusion of sensory information. Jean Piaget, the father of developmental psychology, argued that knowledge emerges through interactive processes of assimilation and accommodation between innate reflexes and the physical world. Yet innate reflexes are relatively primitive, and many have found his theory thus far lacking. But recently, developmental psychologists have come to understand that infants are not so clueless as they might appear, and have a remarkable set of innate skills that, along with experience, gradually develop into the mature abilities that all of us Psi Chi members share – and perhaps some of their parents and loved ones as well.

The skill I have examined extensively in my attempt to answer the question of how we understand size is a curious finding that young infants seem to have a primitive ability to automatically encode the size of an object. This finding was a surprise to a lot of people, because the traditional view was that children do not understand the concept of size until about eight years of age when they are able to use rulers to measure things. But what I found was that infants do notice a change in the size of an object, but only when that object is next to another object that serves the functional role of a ruler. They encode the size of the object as a proportion of that second object. When such objects are not available (such as when you have a glowing ball in a dark room) they can not encode size. Yet when you consider the ecological world of infants, there are plenty of objects in their perceptual world that can serve the role of perceptually-available rulers. A parent, for instance, always walks through the door, and the door itself remains the same size over time, so the infant simply encodes the size of the adult relative to the size of the door. So long as these objects do not change size, infants are able to remember and recall how big or small an object happens to be. Only later, when a teacher or parent shows the child how to use a ruler, do they begin to understand the functional role of conventional standard objects such as rulers, and decontextualize the size of objects from their immediately surrounding contexts. Thus, this primitive ability becomes obsolete and replaced with a new understanding of the concept of size.

But these primitive strategies for encoding size never become obsolete enough. Have any of you ever bought a piece of furniture that looked small in the enormous warehouse where you bought it but once in your home it ended up taking up half the living room? This happened because instead of using your mature adult brain and digging out a ruler or tape measure, you used the primitive strategy from your infant brain and encoded the size of the piece of furniture relative to an available context, namely the size of he warehouse itself. The problem is that the warehouse is much larger than your living room, and thus the piece of furniture appeared a heck of a lot smaller. Only when you bring it home and find it is far too large do you begin to regret the fact that you bought it at a going-out of business sale where there is no hope of a refund! But the point is that as adults we can sometimes see this primitive ability to encode size contextually echoes through our lives and affects us as adults.

But I would like to tell you the story of how I came to this knowledge about infant sensitivity to size. Like many of you, I started working in a psychology lab as an undergraduate probably. I designed an infant study in which I presented babies with sticks of various lengths either inside glass containers or alone on a small stage in a visual habituation task. I predicted that the glass containers provided the role of a perceptually available standard. I spent weeks collecting data that consisted of the amount of time infants stared at the different sticks. Finally, in the lab one night at 2:00 AM, I opened SPSS and conducted an ANOVA on the data. I clicked analyze, and the output showed the following, which, if you took my methods and theory class, you will know exactly what this means F(1, 47) = 5.6, p < .01. For those of you who missed class those days, this means that the experiment worked – I found a real result. I sat there, alone, with my coffee, and just stared at the screen in wonder, because I realized that I was the first person on earth to know this fact about the world. I was addicted.

But not every night has been so lucky. In another study, I spent several months collecting data from infants. I was interested in whether infants could rotate an object in working memory to encode its size. It's not important. I entered the data, hit analyze, and out spat a ANOVA with a p value of .78, meaning I had nothing, nada, ziltch. Three months of waiting for parents to bring in their babies on Saturday afternoons, with many of them not showing up, and those that did often crying in the middle of the experiment and thus rendering their data useless. A lot of sweat and elbow grease for nothing.

The next day I went to my advisor, Janellen Huttenlocher, in frustration. I told her that these goddamn babies were not behaving as they were supposed to. I told her that these infants were ruining my theory. I truly believed that I just had a batch of stupid babies.

She looked at me, in consternation and bemusement, and said, “Sean, the world has spoken to you: Listen to it.” And I realized at that moment that this statement is the essence of what we as psychologists do: we listen to what the world has to say. Many times, it had nothing to say. Many times we asked the world the wrong question. Many times the world speaks a language that we can’t even begin to comprehend.

But when the world does speak to us, and we have the knowledge and wisdom to listen, it usually is says something so fascinating that it is worth all the times that you have to throw up your hands and admit that your presumptions were wrong. Psychological science allows us to understand that we often view the world through myopic lenses; that we might think we understand the way things work and have a theory to explain it, but end up, in the end, being totally wrong. And as disappointing as this may be, this fact speaks to the very complexity of both the questions that we as psychologists wrestle with and the answers we come up with. Even questions so simple as how we understand the concept of size have not so simple answers.

So far, we have waded only ankle deep in this sea of psychological knowledge, and the waters seem warm and inviting. But I also know that we will never really swim far enough out there to answer enough of the unanswered smaller questions so that we can finally answer the question of the meaning of life. But I DO believe that I have come to a better understanding of what the meaning of my life is about, and perhaps a bit of what your lives are about, as well. And it is this: To use the tools of psychological science to come to a better understanding of the world around us, the people within it, and the processes that govern our thoughts and actions. And through this understanding, change the world, inspire the people within it, and help each other maximize all the potential in all of our thoughts and actions.

So I applaud all of you for pursuing an education and career in psychology. I applaud your friends and family for putting up with late night studying sessions and for being guinea pigs in your psychological experiments. I applaud you for doing so well in your coursework and research that you are able to join this elite group of psychologists who are members of Psi Chi. And most importantly, I hope all of you continue to enjoy listening to the world throughout the rest of your lives.

Thank you.

Reviews Blues

So, I seriously got a case of the reviews blues, and I got a tell you, it hurts so bad. I could sing a song about it, to a blues rift. I received a set of reviews from a journal asking me to basically go back to conceptual square one and redesign this entire piece of work. And run more Experiments. Normally, running experiments makes me warm and fuzzy inside, but it is summer, and there are no students around to serve as subjects. So the paper will have to lay dormant until the start of subject pool time.

I recently presented some data at the Association for Psychological Science conference in Washington, D.C. I like the conference because it is filled mainly with people of an experimental sort – not those clinical folks. Not that I have a problem with clinical psych – some of my best friends are clinicians! (I love that excuse) But if another person says, “Are you analyzing me?” when they find out I’m a psychologist…there will be hell to pay. But the highlight for me was meeting my doppelganger – a professor from the Midwest who falls asleep reading statistics books, and not just to read something so boring that she falls asleep, but because she loves statistics. Mmmm. My kind of person! She actually did something really cool – she taught a statistics course that had a service learning component in which the students created this large project to eliminate plastic bag waste. You can read about it here. I’m sold on the idea because I am sick of all the plastic bags crammed in my closet.

So in the meantime, I sit and peruse the internet, when I stumbled upon this great website called edge.com that is a community of people who are much smarter than I am. Every year the host of the website posts a question for people smarter than I to answer, questions of a metaphysical nature. In 2005 the question was the following:

“What do you believe is true even though you cannot prove it?”

The answers to this question are intriguing – and worth reading. (You can find the answers at the Edge Foundation website above). But this got me into thinking how I would answer the question.

My first response is that basically everything I believe to be true I can not prove. I don't even know if there really is anything I can prove to be true, but rather, I can only tell you how likely something I found to be true will replicate if you try to figure it out for yourself. But I believe I am composed of 70 percent water, I believe water consists of two hydrogen atoms and one oxygen atoms, I believe that atoms consist of protons, neutrons, and electrons, and that protons are composed of quarks, and so on. But I can prove none of it. I accept it as truth because I have no real reason to doubt these beliefs, and I don’t see how anyone has anything to gain by foolishly making me believe these falsehoods (perhaps the corporate entity that makes the VitaminWater I drink religiously?) But this is a somewhat unsatisfying answer – a cop out, if you will. The following is a list of some of the things I truly believe but can not prove, but wish I could.

1. Destiny is for the most part a series of random accidents one can not predict

Who are you? I am a cognitive-developmental-cultural psychologist who studies memory, spatial reasoning, and culture’s effects on the mind. I am also a pianist, a painter, a photographer, and on some rare days a writer. But how did it come to pass that these things came to identify me?

That I am now a professor of psychology is a total accident. Once, while an undergraduate at the University of Chicago, I was walking through a building. I could have taken a shortcut through a quad, but I decided to take the longer route for no real reason. In walking down the hallway, I noticed a help wanted sign for a lab technician in a psychology laboratory. Needing a bit of cash, I took the number down, called, and was interviewed and hired. The job was boring - transcribing hundreds of hours of videos of children interacting with parents – but the professor noticed that I worked hard and encouraged me with posing that I work on an idea that eventually became my M.A. thesis.

I often wonder about the person I didn’t become – that moment the universe divided and in this alternative world that person who once was me took the shorter route. I wonder what his destiny would have been. Maybe I would be here (here is a coffee shop in the Bella Vista neighborhood in Philadelphia) or maybe I would be somewhere completely different. Either way, my feeling tends to be that we would like to believe in destiny because it makes the universe seem purposeful. I’d rather simply accept the world I happened to stumble into.

2. People do not differ in intelligence, they only differ in their intrinsic motivation to come up with correct answers

People do not differ in intelligence. This is the great error with our national fetish for testing and ranking, quantifying without truly understanding what the numbers mean. One’s I.Q. score may say something about a person, but it is not any intrinsic and innate level of cognitive abilities. It is rather a habitual and chronic level of motivation for trying hard enough to answer questions correctly.

Now, this claim is in a way is a notational variant of intelligence – you could say that if they both have the same predictive power, why chose motivation over intelligence? However, it is very different from an ontological perspective, and the implications for pedagogy is enormous. You can not change one’s innate level of cognitive ability, but you certainly can change their level of motivation.

3. Babies are far stupider than many developmental psychologists claim, but they have enormous potential

I recently attended a conference in which one fellow was claiming that babies have an innate sense of helping and hurting behaviors, another was claiming that they could solve complex statistical and mathematical problems, and another was saying that infants can judge the intentions of others. Some of these guys I consider my friends. However, I can’t help but wonder why it is the case that a 6 month old infant can solve probability problems, but my 20 year old undergraduates struggle like it is solving Fermat’s Theorem. And as I see it: either the developmental folks are simply wrong, or we get stupider as we get older.

I truly believe that babies start out just like John Locke stated – a blank slate. But not any old blank slate…a slate with lines already carved onto it. These lines are the hardwiring of what will eventually be a rich and complicated system of interacting systems and mechanisms. But there is nothing there are the beginning. There is nothing there in the genes that we can consider to be representational knowledge. And what gets written onto those lines of this blank slate are some kind of universal language that has to do with the universal experience of being a baby – learning to see and perceive the world, act upon and within it, and ultimately, come to understand that the probability of getting heads or tails with the flip of a fair coin are 50-50. We come prepared to learn a great deal about the world, but I can not buy the claim that we come hardwired with a rich set of conceptual schemes.

4. White Capri pants are an evolutionary mistake

White Capri pants universally make anyone wearing them look terrible. I don’t know why this is, but I have never seen someone wearing white Capri pants and said, “Wow, that person looks great!” Perhaps it is something local, having to do with my own fashion preferences, but I think there is more to it than that because I’ve had many a discussion with many a man and have not yet once met someone who hasn’t held the same opinion.

5. You are almost there

This is a fortune from a fortune cookie that I keep in my wallet. I opened this one in Chicago, in China Town, shortly before I left the chains and shackles of graduate school. I believed then that I was almost there. I believe now that I am almost there. And I believe you, too, are almost there. I don’t where there is for me, nor do I know where there is for you, but it is comforting for both of us to know that it is approaching. I hope it is beautiful for me. I hope it is beautiful for you.

Bayesian bar hopping, Einsteinian insanity, and the seduction of soft science

A few months ago I was having dinner with a friend, a professor of physics. We'll call him professor base-rate-neglect. He's one of those hard science jerks who always reminds me that the social sciences are soft sciences. I'm used to claims like these from idiots like him. But, still, I love the guy. So professor BRN was complaining about his love life, or lack thereof. "I don't get it. I'm smart. I'm fairly attractive. I have a good job. But I can't seem to meet women."

Experimentaholic replies, "Well, how are you trying to meet them? Or rather, how have you met the women you've dated most recently?"

Dr. BRN says, "I met Kelly at a bar. That ended horribly. I met Jen at the park. Ended terribly. I met Susan at the bookstore. Ended because she moved to Oregon."

Experimentaholic: "Well, have you ever heard of a guy names Thomas Bayes?"

BRN: Sure. He did Bayes Theorem. I forget about what it says, though. I hated statistics. It's soft math.

Experimentaholic: I hate it when you people say that. Especially since I will use soft math to solve your problems. Bayes dealt with a statistical problem having to do with where billiard balls would end up resting on a table. I think this directly relates to your problem.

BRN: This is why I don't trust you soft scientists. Soft thinking. Billiard balls. What do billiard balls have to do with my love life?

Experimentaholic: More than you'd think. I won't go into the gory details of marginal and conditional probability, because you probably slept through stats. But let me ask you another question. How many times per week do you do any of these activities?

BRN: Well, I might seem a bit like an alcoholic, but I probably go out to bars three times per week. I go running on the weekend, and probably go to the bookstore once a month or so.

Experimentaholic: Okay. Think for a minute. So you go to bars 12 times a month, and you got one hit and 11 misses. You go running four times a month, and you get one hit and three misses. You go to the bookstore once a month, and you get one hit, no misses. Do you get where I am going with this?

BRN: Not really.

Experimentaholic: Dude, for every time you go to the bar each year, say, there is a less than one percent chance you are going to meet someone. Why? Because you head to the bar 144 times per year, and only have one relationship to show for it. You go running 36 times per year, and you have one relationship to show for it. That means the probability of you meeting someone while running is around 2 percent. Now, you go to the bookstore 12 times a year, and you have one relationship to show for it. That's an 8 percent chance that every time you go to the bookstore, you'll meet someone.

It seems as if you're doing everything backwards. What would Thomas Bayes do, if he either were alive today or not a Presbyterian minister, or not a [explicative deleded] lush like you? He would be going to the bookstore 3 times a week, going running twice a week, and avoiding bars altogether. Man, you got your strategies mixed up. All because you are ignoring the base rates - or the hits and misses - of your strategies of meeting people.

BRN: I never thought of it that way.

Experimentaholic: I know you think that my kind of science is soft, and that psychology is bullshit. I think a lot of psychology is bullshit too. But I am forcing you to do a little experiment. I don't care if you keep going to bars three times a week, you're a lush after all, and the tenure track thing is stressful. Drown yourself in beer. But I am forcing you to go to the bookstore three times a week. An hour at the bookstore, perusing the shelves, and let's see how your love life changes.

BRN: We'll see. I'll have to think about it.

Experimentaholic: Think all you want. It's the fact that you're not thinking about base rates that makes you miserably unhappy and sitting here complaining to me, and going home alone to your miserable apartment and crying your lonely self to sleep.

BRN: Whatever, you [explicative deleted] soft scientist.

Now, I haven't seen BRN for a little while, and I just received the following email from him.

Experimentaholic:

Yo, man. Sorry I've been out of touch, but the most amazing thing happened. So at first, I basically ignored your little "experiment" and kept doing what I always do. I thought, "You're dumb, and what do you know?" Then, a few weeks later, after a pretty bad hangover, I decided to try your little experiment. For two weeks, I went to the bookstore three times a week. During the third week, I'm sitting there, reading a copy of Dawkins's The God Delusion, when this totally gorgeous woman walks up and says that she loved that book. We started chatting, and she is a biology grad student at [redacted] university. We totally hit it off, and she gives me her number. I call a few days later, we go out on a date, and you know where this is heading. Long story short, I'm seeing this girl. It's been five weeks now, and I am totally falling for her. Man, I can not believe that a psychologist of all people could [increase the frequency of his sexual encounters]. I thought you soft scientists were idiots. Next time we get together, dinner's on me.

My response?

I guess it takes a psychology professor to remind a physics professor that Einstein defined insanity as "doing the same thing over and over again and expecting different results." Perhaps there is something to soft science after all? Either way, I will relish the dinner. And I look forward to meeting the new lady.

Experimentaholic saves the day.

Prediction and postdiction

I share in the horror over the massacre at Virginia Tech. Part of the shock for all of us in academia is that we tend to think of school as the diving board of life: a place where lives begin, not end. I see my own students and colleagues in the images of both the victims as well as the perpetrator. And that both saddens and terrifies me.

However, I find it upsetting that people are criticizing Virginia Tech for ignoring warning signs. I find that response represents a severe and all-too-common error in thinking about direct versus inverse probability.

The basic premise rests in the fact that the following statements are not identical:

1. Given person A wears a trenchcoat, is quiet, and writes plays involving murder, there is a high probability that he will go on a shooting spree.
2. Given person A went on a shooting spree, there is a high probability that he wore a trenchcoat, was quiet, and wrote plays involving murder.

The first statement is one that is a matter of direct probability. You multiply the proportion of people who wear trenchcoats, who are quiet, and who write plays about murder, and you get a number which represents the proportion of the population that are going to go on shooting sprees. However, there is a little problem: a lot of people wear trenchcoats, are quiet, and write plays about murder. Round them up, and you might find a group that includes a significant proportion of the undergraduate population. However, a significant proportion of the undergraduate population will not end up going on a shooting spree. That concerns the error inherent in mistaking direct and inverse probability.

A 17th century minister named Thomas Bayes noted that probability of event A conditional on B is generally different than the probability of B conditional on A. Bayes came up with a solution that links them mathematically by a simple equation called Bayes Theorem. In short, the theorem explains that the relationship between direct and inverse probability is a function of the base rate, or frequency, of the two events. Psychologists have long known that people ignore base rates, resulting in serious errors in reasoning that can be fatal.

For example, there are many cases of heterosexual, non-IV drug users who killed themselves because they received news of a positive HIV test. Their doctors probably informed them that the HIV test has an accuracy of 99.99 percent. However, that does not mean that they can be 99.99% sure that they have HIV. Why? Because of the base rate: tens of thousands of people take the HIV test, and HIV prevalence is extremely low (about 1 in 10,0000) among that particular population (heterosexual non-IV drug users). Every once in a while, given the fact that tens of thousands of tests are run, a negative sample will test positive (the 0.01 percent inaccuracy part). So the actual probability of being HIV positive given a positive HIV test (again, if you are a heterosexual non-IV drug user) is actually about 50% (I calculated this using Bayes Theorem). But most doctors I've interviewed never even heard of Thomas Bayes or his theorem, and make the same mistake their patients do in assuming that direct and inverse probability are the same.

In a similar way, it is easy to say, after the fact, the postdiction that someone should have known, that someone should have done something, that the university was irresponsible for not having seen the warning signs. But the problem with these statements is that they ignore the base rate of the frequency of these warning signs. A lot of college students show warning signs, and many students show warning signs that are considerably worse than those exhibited by Mr. Cho. And unless one were to come up with a better diagnostic tool than trenchcoats or murderous plays - like a crystal ball - I don't believe it is possible to predict who is just an awkward student (of which there are many) and who is going to be a serial killer. I hope we someday can tell them apart, but knowing a bit about human nature - and the way we make errors in our reasoning about probability - makes me doubt it.

Experiments in Punditry

I recently appeared as a talking head on an hour-long cable news show concerning a bill introduced in California that would ban spanking. I was asked if I would make some points as to the limitations of the bill, which I agreed to, so long as I could clarify that I was anti-spanking and that there are many alternatives to corporal punishment that are more effective and less harmful.

But then what problem do I have with a bill banning spanking? Well, basically I believe that an ounce of prevention is worth a pound of cure. If we as a society really care about children, we should teach children how to be good parents – by being good parents ourselves, and by developing programs that teach pregnant women and their partners and families about the challenges of raising children, and how to deal with all the stresses inherent in being a parent. To intervene AFTER the spank has occurred, as this law does is pointless – for whatever harm is inherent in spanking (if any) is already done, when the entire harm could have been avoided in the first place if we only took the steps of educating people before the harm occurs. Also, there are many people who are unfit to be parents, and they need to be discouraged from fostering children until they are ready to be assume what amounts to one of the most difficult social roles imaginable.

We could go on for hours about semantic issues related to the meaning of a spank versus abuse, ontological issues related to what is discipline and punishment, teleological issues related to what is the aim of good or bad parenting, epistemological issues related to how we learn to practice parenthood, and so on. That is an issue for another blog.

My main concern has to do with the use and abuse of research to put forth an agenda and the nature of scientific objectivity. The other guests with whom I was discussing these issues, while I respected their thoughts and viewpoints, all had some agenda. For instance, one was a member of the Family Research Council, a Christian conservative think tank. The other owned a company that runs programs that teaches parenting skills. What struck me was the extent to which these individuals were emotionally invested in the issue. I never really thought much about spanking, because there seems to be larger issues at hand – pardon the pun – such as child physical and sexual abuse. But I respect that in certain cultural contexts, spanking is a normative practice, and even if in some cultures it may not be prescriptive, to apply a universal standard would be to ignore the fact that parental discipline occupies a complex cultural space in which various factors – cultural, social, educational, economic, sociological, and so on – intersect. The inner workings of the family is not a sphere in which a “one size fits all” policy seems appropriate.

I have always taken issue with extremes. “Anything goes” and “Nothing goes” seem to be fruitless approaches towards thinking through most problems. But I believe that the vast majority of people, the vast majority of the time, shy away from thinking through an issue but rather feel through it. Steven Corbert was onto something when he popularized the term truthiness. Most people’s convictions are based upon how they feel, not how they think, and often what we feel we should do, and what we really should do, are in stark contrast. Too many people trust their guts, and unless you are a gourmand, you probably should question what your stomach tells you.

So it was kind of fun to be on television. They had a make-up lady do my face and hair - it was the first time I had to wear makeup since that time in graduate school when I went to a party in drag. There were lights and cameras and satellite hook-ups and all sorts of interesting things. I went into this with one thought in my mind: “Imagine the hypocrisy of a state that practices the ultimate form of corporal punishment – the death penalty – trying to outlaw spanking.” It didn’t set well with the liberal side of me. But neither does spanking children. I do regret one thing that I said…that one alternative to spanking is distracting children – that children have short attention spans and that if they want to touch a hot stove, to distract them with something else, like the television.”

I want to officially say here that I think that spanking is far better than forcing a child to watch the garbage that counts as television these days. I had a nightmare last night of parents following the sage advice of Professor Experimentaholic and putting their children in front of Bill O’Reilly's No Spin Zone. Now there should be a law against THAT. I'd be the first in line to vote for that.

At another level, I guess I am being a bit hypocritical because I say this after having appeared on television myself. Oh well.

I don’t think I would ever make a very good pundit. Pundits tell you what to think, not how to think. Pundits tell you what is right from wrong, not how to determine for oneself what is right and wrong. Any bit of knowledge or wisdom that I could tell you in 30 seconds or less is probably not knowledge or wisdom worth having.

But what I didn’t get to talk about is the nature of the research on corporal punishment, the vast majority of which is fundamentally flawed. The main flaw comes in the form of mistaking correlation for causation. The vast majority of these studies do something like this: Get a group of parents and ask them whether they spank their child, or how frequently, or how hard. Then they measure behavioral problems in the two groups of children, do some multiple regression with dummy variables, and find that children of parents who spank them exhibit more behavioral problems. Then the wise researcher then goes and says that spanking causes behavioral problems. The problem with this approach should be apparent immediately to anyone since Aristotle’s Metaphysics. With this quasi-experimental design, you can not say that the spanking causes behavioral problems because it is equally possible that children with behavioral problems are more likely to get spanked. To do the study right, you need to take a group of new parents, and divide them into two groups – one who spank their children, and one that is prohibited from spanking, and measure the outcome. However, quite fortunately, I doubt there is an institutional board out there that would be willing to allow researchers to tell a group of women who wouldn’t spank their children to do so, and with vigor!

So we are left with some pretty questionable causal links. (There are a number of other problems I won’t go into, such as the fact that parents who spank their kids also are more likely to abuse them, which is not to say that spanking is a gateway practice into abuse, which is again another causal misinterpretation). And I don’t mind studies with poor causal links: they lead you down the path to more careful empirical investigations. My only fear is that given this fact, people – people with Ph.D.s and official-sounding titles at important-sounding institutions who really should know better than to pull this kind of nonsense - seem willing to make sweeping interpretations and inferences based on this paucity of available data. And the only rationale I can come to is that they were convinced of interpretations of the data long before they ever looked at any data of any kind. It doesn’t matter what the data says when you approach it with the zealotry of a pundit. You’ll find what you want in it – it will be like a Rorschach test. And you will always find what you want in your data when you have a vested financial or spiritual interest in the outcome. It’s not even worth citing a study, or citing research, or even pretending that you are even doing science at all.

I caution the reader, as I caution my research methodology class, that warning bells should start ringing in your head when any talking head says, “Research shows that…” or “Studies have determined that…” or variants thereof. What research? Which studies? Are there studies that show the opposite effect? Who did them? Who funded them? How were they collected? Who were the participants? Who were the interviewers? What scales were used? The devil is in the details, and I don’t want to start basing social policy or law or putting people in jail or funding some guy’s company that teaches parenting skills based upon poorly constructed and controlled quasi-experiments. Or worse still, evaluations of former participants of such programs. Or the fact that the president of this company has several lovely children who he never laid a hand upon and who have grown up to become well-adjusted productive members of society. This isn’t evidence of anything. But to parade this as evidence seems to me to be about as dubious as the kind of claims made by alternative resistance exercise machines, diet pills that will make you lose 10 pounds a week, and dead Nigerian kings whose heirs have to remove $10,000,000 from the country.

If I had my thirty seconds of sage advice, it would be this: I think one needs to have an open mind, but not so open that your brains fall out. Likewise, it is useful to have convictions, but you shouldn’t let those convictions lead you blindly down the road to conclusions. And it is easy to be a talking head, but a head not attached to a solid body of empirical data and carefully designed research should have its microphone turned off.

Notes from a fellow experimentaholic

One of the world's most famous experimentaholics was the British polymath Sir Francis Galton. Galton had a fetish for measuring, and he measured everything, from people's heights to their attractiveness to their intelligence to their fingertips. It was galton who first came up with the notion of regression to the mean, a common occurance such that people who do well on a test tend to do worse the second time one takes a test, and those who do really bad improve on the second. This has to do with the fact that people who do very well are smart, plus had a little luck. Test them again, and they may not be so lucky. Galton came up with the correlation coefficient and other handy statistical tools. He also was the father of eugenics, something perhaps not to be so proud about.

However, in leafing through issues of the journal Nature from a hundred odd years ago, I found this curious little solution to a common problem: the fact that one can have one's cake and eat it too, but not having the appetite to finish the whole thing. The problem is that those cut parts that lay exposed to air get stale. A common problem. Well, apparently, a "F.G." devised the solution described in the following Letters to Nature section. On further investigation, I discovered that our curious cake consumer F.G. is none other than Francis Galton himself!



This goes to show - it was easier back in the day to get something published in Nature. If only that were the case today!

Principles of indifference

It’s happened to you, I’m sure, as it has happened to me. You go about your life, working on your computer, editing files, processing data. You don’t get up in the morning thinking that today will be the day. The day that you fire up your computer, with all the hopes of getting that paper written, and instead are faced with the Blue Screen of Death. A message blinks “Can not find hard drive” or something equally vague and frightening.

It happened to me one winter evening in Ann Arbor, Michigan, where I was a post-doc. I hadn’t backed up any of my files for about six months. I restarted my Mac after it wouldn’t connect to the internet and . . . it never started again. Blank screen. I took it to dealers, tech support…nothing. Someone offered $5,000 to try and salvage the data off the hard drive, but I figured it wasn’t worth it. I could start from scratch, having learned an important lesson. But I lost hundreds of hours of time rewriting papers, reanalyzing data, and piecing together all that I had lost. Fortunately, some of the stuff was recoverable – colleagues who had drafts of manuscripts emailed me the files. But a lot was lost forever.

I ran into our friendly computer tech support director Harold the other day. It is because of Harold’s relentless campaign on backing up data that inspired me to burn all my work onto a CD every week. But it makes me wonder about the psychology involved in backing up one’s data. Even after my experience, I still don’t always back up my data. Some Fridays I just feel like going home – “I’ll do it tomorrow.” And I suppose one of these tomorrow’s I will fire up the machine and get that screen of death.

And who will I call? Harold. And often, what can Harold do? Nothing. This is not because Harold isn’t a great IT person – it is because Harold isn’t Zeus and can not pull a dues ex machina, coming down to earth and intervening with the ones and zeros that constitute the information on the hard drive.

I recently wrote a post about LaPlace’s 1822 Rule of Succession. Gigerenzer talks about a related notion to the Rule of Succession known as the Principle of Indifference. It basically has to do with what probability you assign to the possibility of an event given no prior knowledge. Recall my discussion of HIV infection – you can apply Bayes Theorem to situations in which you know the base rate – or frequency of – an prior probability, such as the proportion of people of a certain population that is infected with HIV. However, when you don’t know this prior probability, you are faced with a situation of indifference in which you assign equal probabilities to the likelihood of an event.

Electronics tend to follow an inverse power law in terms of their life-span. That is, take a hundred iPods. Once they leave the factory, 100 of them work. A month later, 99 work (i.e., you may have dropped it in the toilet by accident). A year later 80 of them work, and so on, until only 1 is still working some years down the line. And this is okay, because electronics are replaced with newer gadgets. But it is the probability of failure I am concerned with here: All electronic devices will someday fail. But why are we so confident that on any given time that you shut down your machine without backing up your data, that tomorrow when you start it, that the machine will in fact work rather than result in the blue screen of death.

I think the answer has to do with the law of succession, the same problem faced by Adam and Eve in the Garden of Eden. When you first buy your computer and turn it on, it is as if your computer gives you a white marble which you place in a box. Already in the box is a Blue Marble of Death, because you don’t know whether or not it will ever turn on again as it could be a lemon. Every time you start your computer and it works, your computer gives you another white marble from its box which you place in yours. Eventually your box will contain a lot of white marbles, representing your confidence in your computer.

But your computer doesn’t see it this way. Your computer is doing something different. It starts off with a lot of white marbles in its box, and one blue marble of death. And every time you turn it on, it selects a white marble from the box, and doesn’t replace it – it gives it to you, improving your confidence in it. So it may begin with a thousand white marbles and one blue marble of death. And the next time you turn it on, it selects a marble from its box. With high probability it is a white marble. But with every successive selection from this box, the probability increases and increases that the blue marble will be chosen until that day when suddenly, and unexpectedly, you turn on the computer, with a very high confidence in it working, while simultaneously, the computer selects the blue marble.

The result? You’re screwed.

The following figure provides a depiction of the expected probability that you have that your computer will start given a certain number of prior starts (by the rule of succession), the expected probability that your computer will select the blue ball of death randomly without replacement on any given start up. And then we encounter the real world. This hypothetical computer selected the white ball of hope all the way up to reboot 77. Then, on reboot 78, the computer selected the Blue Ball of Death, and CRASH! There went your work (unless you backed it up).

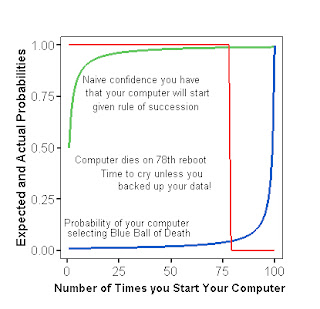
Do we reason this way? People are bad as assessing the probability and success and failure, which is why do many people gamble despite the odds. Hope springs eternal in the Garden of Eden, in Atlantic City, and in your office. But even with all the hope in the world, there comes a day when your luck runs out. It could happen on the 78^th time, on the 788^th time, or the 7888^th time. But it WILL happen. And you can either lose three hours of your life, or three years.

Your choice.

Hope springs eternal in the Garden of Eden

I was speaking with a friend yesterday about relationships. The conversation we were having was about the fact that just because your last relationship was bad and ended bitterly, how does that influence how you think about future relationships? Not all relationships end in misery, right? ("Just mine" you might be thinking...)

I suspect that the solution to this problem can be found,as always, in an unexpected place: probability theory. There is an appropriately-named statistical problem discussed by the French mathematician Pierre Simon LaPlace (1749-1827) called the “First Night in Paradise." Basically it goes like this:

It is the night after Adam and Eve’s first day in paradise. Together, they watch the sun rise and illuminate the marvelous trees, flowers, and birds. At some point, the air gets cooler, and the sun sank below the horizon. Will it stay dark forever? Adam and Eve wonder, What is the probability that the sun would rise again tomorrow?

Whether Adam and Eve were truly discussing this statistical conundrum, as opposed to addressing less cerebral concerns of a non-probabilistic nature, is besides the point. What is the probability that the sun will rise again?

The classic answer is that if Adam and Eve had never seen the sun rising, they would assign equal probabilities to both outcomes. Gigerenzer, in his book Calculated Risks, likens it to placing a white marble (the sun will rise again) and a black marble (the sun will not) into a bag, and picking one randomly. However, they did witness the sun rise once that morning when they woke up, so they place another white marble in the bag, which makes the probability of the sun rising the next day .66.

(Interestingly, as an aside, one might ask the question, "What was Adam's subjective assessment of the probability that Eve would still be there the next morning?" After all, she did simply just appear there, and who knows? God might just be teasing him and yank her out of the garden.)

As we, know, Adam and Eve woke from that first night in paradise to another sunny day in paradise. But what is the probability now, given two sunrises, that the sun would rise once again the next day? The answer is simple. They add another white marble to the bag, making the probability go up to .75. And the sun rises again and another marble goes in the bag, and so on. This is known as the rule of succession. Introduced by LaPlace, it has a simple formula:

(n+1)/(n+2)

If you are like me, and are thirty odd years old, the subjective probability that I assign to the sun rising tomorrow is quite high. Specifically it is

(365*30 + 1) / (365*30 + 2) = 10951 / 10952 = .99990869247626004. Pretty good odds. I am, in fact, relatively convinced that the sun also rises tomorrow.

But what about relationships? Does the law of succession apply here? What is the probability, given a certain number of previous relationships, that you believe that your next one is headed to splitsville? It is just like adding white balls representing sucess and black balls representing failure to a jar and selecting one.

I asked ten friends and colleagues today how many serious relationships they had been in over the course of their lives. The median value of that number was 7 – your typical friend of mine has been in 7 serious relationships (which I defined as lasting over 6 months).

What is the average person’s subjective estimate of the probability of the next relationship ending given the rule of succession? Quite simple: (7 + 1) / (7 + 2) = 8 / 9 = .888.

So is it the case that with a greater number of failed relationships, does one use the law of succession to determine whether one’s next relationship is going to fail? Maybe. This would be an interesting study to conduct – the correlation between the number of failed relationships one has had with one’s pessimism about the probability that one’s next relationship is also going to fail. Of course there are confounds up the wazoo, but it would be a fun and simple study to do on a larger scale than my ten friends.

But there is hope here. While you might suspect that your next relationship will fail with a probability of .88, that means that you also have a probability of .12 that the next one will work out. And I like that 12 percent – I might like to call it a “Hope Factor.” Sure, the hope factor diminishes after every successive failure, but by definition, this means that one can never lose hope entirely – the law of succession may asymptote very near zero, but it never quite reaches it, due to the fact that the denominator is always one greater than the numerator. Below is a figure of the relationship between the hope and despair factors by the number of failed relationships. You can see how the region of despair increases with every sucessive failed relationship, but that region of hope never quite goes away.

As they say: Hope springs eternal! And perhaps this is why it was the last evil remaining in Pandora's Box.

The possible and the probable

I spent the last few days at the National Science Foundation reviewing grants. Truth be told - you know you're nerdy when you walk into a restaurant after having forgotten to remove one's NSF temporary ID badge reading "Hello, my name is experimentaholic." and are reminded of this fact by an attractive yet not-so-nerdy restaurant hostess. Reviewing grant applications, in and of itself, in not very much fun, because I simply don't like being the one who decides who gets funded and who doesn't. I think everyone should get funded, myself included! But this is not the state of affairs - only some get funded, others get the apology letter. And I've gotten my share of those thin ones.

Which brings me to the topic of the probable and the possible. What does probability mean? For instance, these people who wrote grants submit them, and there is a certain probability that they will get funded, which is based on how much money NSF has to dish out. They also have a certain expectation of the probability that their grant will get funded, which may differ from that which is actually possible given the availability of funds.

But what does it mean to expect an event with a certain probability? Like dying on a plane crash. The probability of this event is quite low - something on the order of one in eight million. So we get on the plane, and most of the time, get off the plane. But when you get on that one plane that explodes, and you ARE that one in eight million, the probability is not quite 1 but certainly close to it. But what does uncertainty mean, at least at the level of a psychological construct?

I know that there is a lot of evidence on this - and most of it points to the fact that people are particularly bad at assessing probabilities and changing their behaviors based upon these assessments. People drove after 9/11 out of fear of flying, and this increase of traffic and the resulting accidents that ensued killed more people than had died on the planes of 9/11. True! I buy a lottery ticket when the powerball is in the hundreds of millions, realizing full well that the probability of actually winning is the same as correctly guessing a random a number between zero and 120,526,770.

I am at the moment in a coffee shop, it is a Friday night, and two students next to me are discussing Spinoza, and specifically free will. This makes me wonder about our free will in relation to our assessment - and flawed assessments - of probabilities. I have always dreaded flying, even knowing that the probability of dying is the same probability of guessing a number correctly between zero and eight million. But what if I am just lucky (or unlucky) that day? Everyone who has ever died in a plane crash has gotten on that plane imagining that the probability of a crash was one in eight million. Which is fine, if you're a member of that elite group of eight million. But if you're not, not.

One way to think about it perhaps is actuarially. When you get on a plane, you have to think of the degree to which taking this trip will actually reduce your life. A related situation is when you buy a lottery ticket. A lottery ticket is really worth what you paid for it, plus whatever the probability of winning the ticket multiplied by the reward. Imagine the senario of the powerball. The ticket costs $1. The jackpot is 100 million But the real value of the ticket is $1 + $100,000,000 X 1/120,526,770. Which is $1.82. Of course, afterwards, any given ticket is either worth $0 or $100,000,000...but in the seconds before the balls drop, it is worth $1.82. What about one's life? The probability of dying in a plane crash is 1 in 8 million. As a thirty year old, I expect (or I should say hope) to live another 30 years at least. More would be better. 30 years comes out to 946,080,000 seconds. But by getting on that plane I am reducing my life by 946,080,000 seconds X 1/8000000 or 118.26 seconds. Of course, after the plane lands or crashes, that amount changes to 0 seconds or 946,080,000 seconds. Is it worth it? Does this way of looking at the problem solve the problem, or just create new ones?

Which brings me back to free will. Does the fact that we live in uncertain world make it such that our free will is compromised? I don't know. How does our inability to reason about probabilities affect our decisions? Probably in some domains, probably not in others. Some people are notoriously bad at making comparative judgments of probabilities and possibilities - those who drove rather than fly after 9/11, who are now in the grave or scattered to the winds because their dread risk overcame their rational capacities.

In this sense, statistical probability and mental probabilities must be related, but they are not homologies. Keyes wrote something about this, on personal probability, but I confess I haven't read it, yet. Perhaps I'll read it someday. It's both possible and probable.

I'll have some love with that microscopic $9.95 piece of salmon

A student of mine once did an experiment using this web site called "Craig's List Missed Connections." Basically, it is a site in which people post notes to the universe that say things like, "I saw you walking down the street and you glanced at me. You were wearing a red hat and a green scarf...coffee?" And so if you think you are this person you can email this individual back and hopefully begin a life of love and lust together. That, or realize you have absolutely nothing to discuss over coffee.

Recently I was reading this site (perhaps perversely to see if someone posted something about that guy in the coffee shop cursing SPSS under his breath when the p value for his most recent experiment is greater than .05.) One thing I’ve noticed in passing through these listings is how there are many posts about missed connections at Whole Foods - the local hip foodstore in my neighborhood.

But this has gotten me into wondering…what is it about Whole Foods that inspires people into longing? Is it something about the air of an organic, expensive grocery store that makes people lust after strangers? Is it that only well-to-do people who can afford well-to-do people’s clothing and well-to-do people’s makeup and well-to-do people’s hair styling can afford shopping at the place? Or is it a unique place in this world - a world in which we communicate so often over the internet that we no longer know how to approach a stranger and say hello, but have to go back to our internet world and post a little "I think I saw you looking at me, but I am not sure and I'm oh so insecure!

(Here I would like to add that such people should read the excellent paper by Clark and Hatfield (1989) in which they had experimenters go around Florida State University's campus and randomly ask strangers if they would go out on a date with them that night. Something like 60 percent said yes! Could be something unique to Floridians, though.)

I wanted first to determine if there was an effect at all. I did a quick search and found that in the past 45 days on craigslist there were none less than 37 postings of missed connections at whole foods. But right next door to whole foods is a regular old supermarket known as Superfresh. How many quick glances and subtle smiles have been exchanged there? Only 8. And this includes all the Superfreshes in the city.

I figured I would try different cities. Let’s try Ann Arbor, Michigan, which I know has a Whole Foods because I used to shop there. They also have Kroeger’s, the Ann Arbor equivalent to Superfresh. 1 hit for whole foods, none for Kroeger. I tried Chicago…5 for whole foods, 1 for Dominick’s (there are dozens of Dominicks out there)

What is the probability that this could be due to chance? I'll stick to the Philadelphia one because it has the most data. Imagine that it were purely due to chance that sightings would occur at Whole Foods and at Super Fresh. Then the expected probability would be .50 - a fifty-fifty chance. What we observe is 8/37 or a 0.21 percent sightings at Superfresh. What are the odds that this is due to chance? Luckily, we have the good old binomial test to tell us the odds. The actual probability that this could be due to chance is 0.000007687045. That's a very small odds! There is something fishy going on, and I don't just mean the salmon I ate for dinner. That I bought at Whole Foods.

I suggest you experimentaholics and statistiphiles try this in your own cities. And if I see a post for that guy talking about Chi square at the produce section, I’ll know I’ve finally been missed.